哈哈又开新坑了。
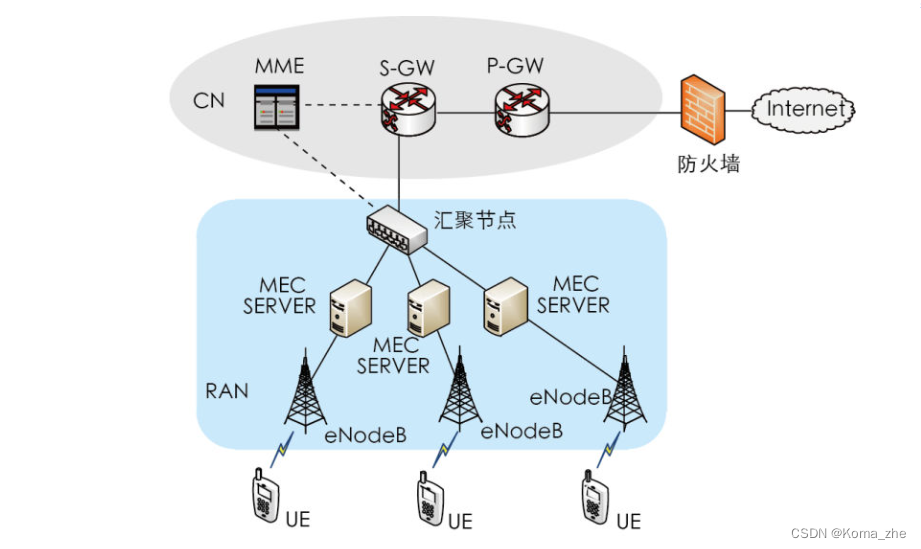
我目前刚刚开始调研这部分的内容,下面是我的第一印象:场景是终端、边缘、云服务器,强调资源的卸载,许多边缘计算+SC的论文专注于MSC,MSC用通俗的说法就是部署在移动通信系统的基站附近的服务器,为什么要用语义通信呢?因为大量任务卸载时需要极高的传输速率和吞吐量,并且要考虑到能效、延迟和数据隐私。
《Semantic Communication in Satellite-Borne Edge Cloud Network for Computation Offloading》
场景:SEC(星载边缘云)
用户和低地球轨道通信可以用C 波段用户卫星无线电链路或者先通过与 TST (地面站终端)之间的C波段链路和 TST 与 SEC 之间的 Ka 波段链路,通过 TST 接入 SEC,后者也是OFDMA的方法。
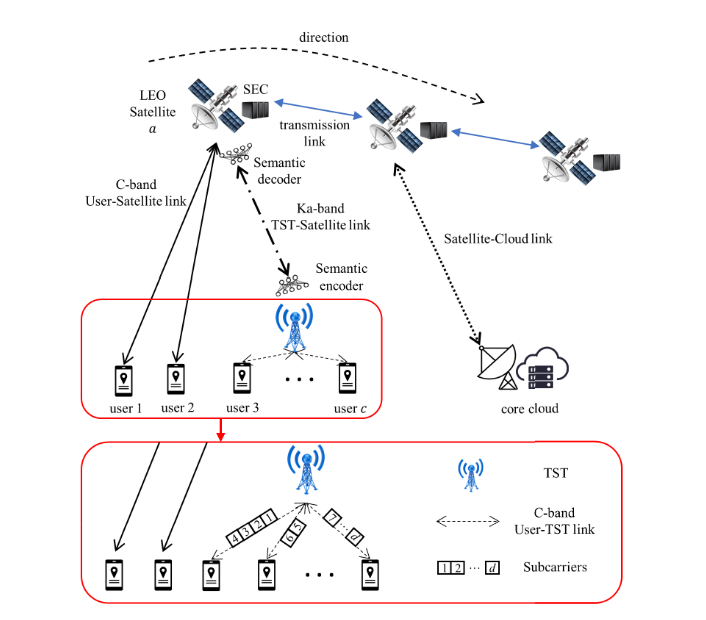
这篇论文主要提出了两个架构。
一个是PSFed,用于控制TST和SEC的编解码器联邦训练过程,考虑到TST本身的数据隐私,TST 本地用私有数据训练编解码器,算编码器“重要性”→只上传重要的编码器位点 +(解码器全量)→SEC 对“上传位点”做编码器聚合、对解码器做全量聚合→下发“全局解码器 + 为该 TST 定制的裁剪后全局编码器”→TST 替换解码器、仅覆盖编码器的重要位点→继续本地训练。这就是段落中所谓“剪枝≠删除,而是‘不传’低重要度参数”与“个性化编码器 + 全局解码器”的核心逻辑。
一个是CTPS,训练好的语义编解码器投入业务后,用户需要在“本地计算 / 直连卫星上 SEC / 经 TST 至 SEC / 直达云 / 经 TST 至云”五条处理路径之间,联合考虑时延–能耗–隐私–公平作任务调度。直接建模得到的是一个因隐私导致信息不完全的 MINLP(式(36)),难以求解。
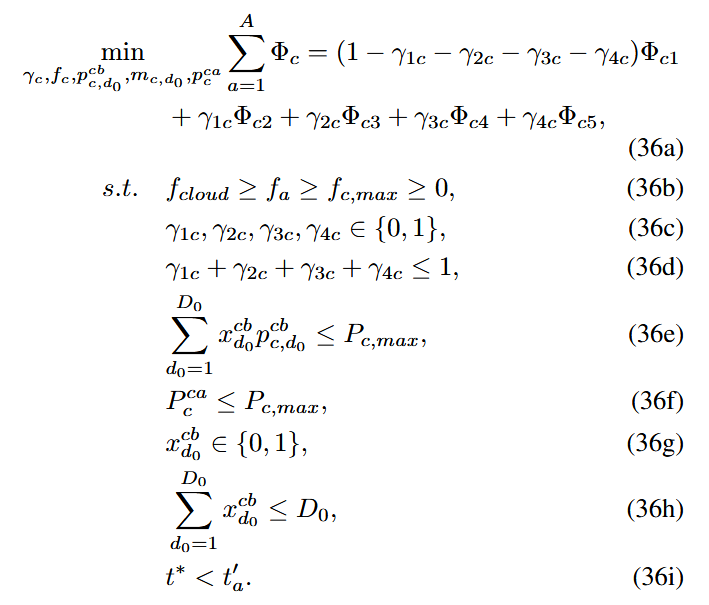
CTPS将其分成两步:(i)用Rubinstein 议价博弈把“缺信息”的问题转化为完全信息;(ii)在完全信息下把式(36)分解为可解的子问题并用拉格朗日对偶分解求解。
参与方与轮次:用户与 TST 进行至多两期的议价/沟通;TST 充当出价方,用户可选择继续或退出。第 1 期中,TST 按用户申请卸载任务的大小为其公平分配 C 波段子载波数,并同步通知“TST→卫星传输时延与语义提取时延”。这样做的目标是在不泄露能力或功率等隐私的前提下,让每个用户拿到后续优化必需的“资源分配信息”。
为何使用 Rubinstein 模型:交替出价 + 折现的 Rubinstein 序列议价存在唯一的子博弈完美均衡,折现因子刻画“拖延的代价/耐心程度”,可用于构造公平且激励相容的资源分配(本文用它来公平分配子载波并最小化信息披露)。
问题分块:式(36)可视作 5×A 个独立子问题(5 条处理路径 × 备选卫星数),分别求每条路径在各卫星下的代价,再选最优路径与接入点。拉格朗日函数(式(41))与对偶分解:对功率约束与任务守恒分别引入乘子 问题被分解为 D0个相互独立的子载波子问题;KKT 条件(式(44))与互补松弛**(式(45)):来解决这一凸问题。

