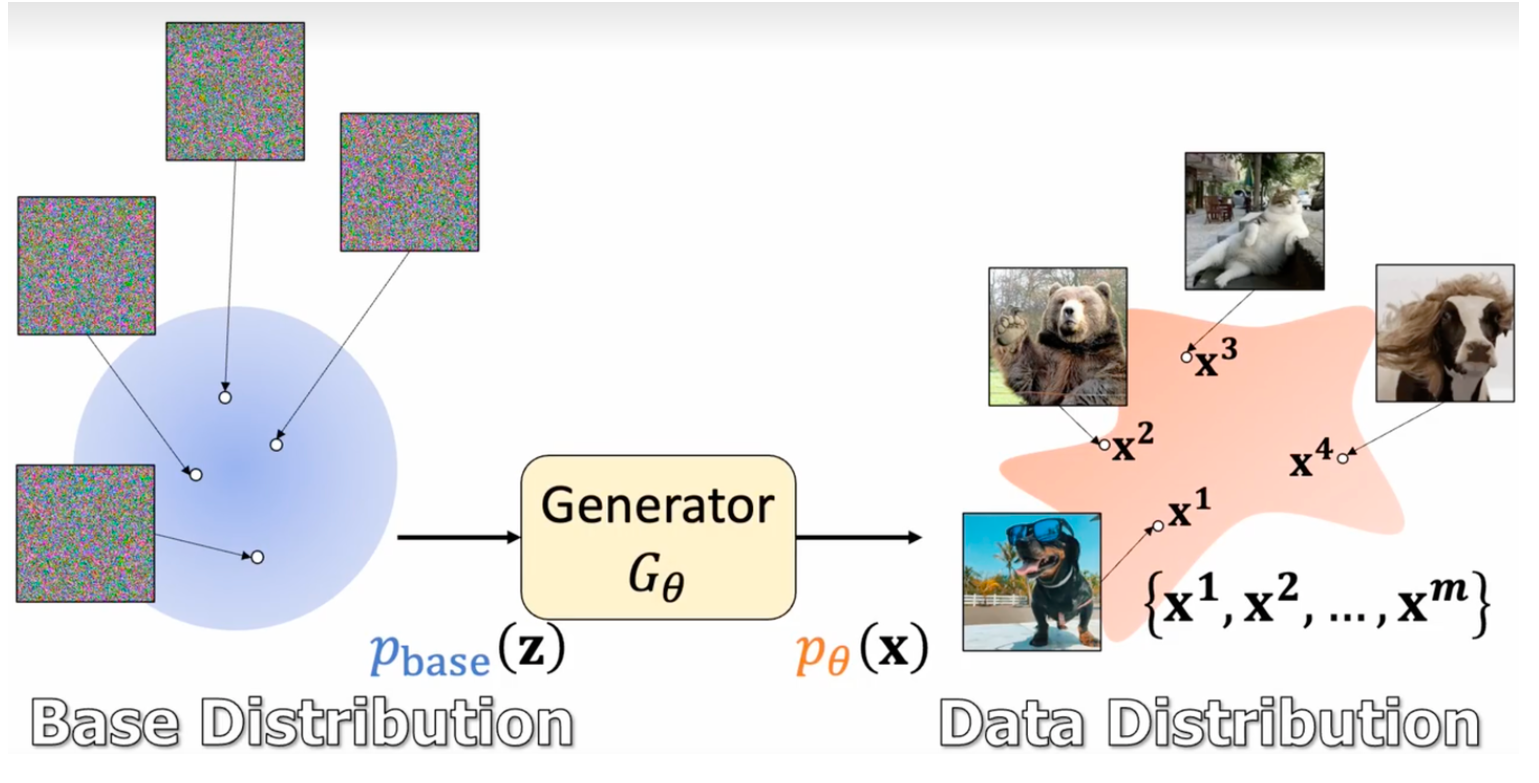
Flow Matching是一种生成式模型。
最简单的生成式模型,目标就是没输入的情况下,就能生成与给定目标集中的样本相近的样本。
带条件的生成式模型,网络学习的是映射。
diffusion算法,则是学一种降噪算法,它会自动判断图片中的噪声是啥,并尝试恢复原图。但如果直接一步用一张全是噪声的随机图来生成原图,则依然存在前述可能性过多而导致结果是多种可能均值的问题,因此,diffusion会进行初步的降噪,然后再尝试根据降噪的输出结果作为输入,再次尝试降噪,这次降噪时,因为已经有了前次的输出作为输入,更多的输入把结果坍缩成了少量的状态。这样经过多次迭代降噪,结果越来越坍缩,就规避掉了前边的结果为均值的问题。
特别的,假设我们要生成的Pdata都是在[0, 4pi)区间内的y = sin(x)曲线上的点,那么,我们想训练一个模型,希望能让这个模型学习到这些点的特征,并能够生成一个满足这些特征的任意的点。Flow Matching算法,要学的是一个行驶(修正)的方向,即,如果我有一个点,可以移动,我该怎么走,才能走到目标点上。
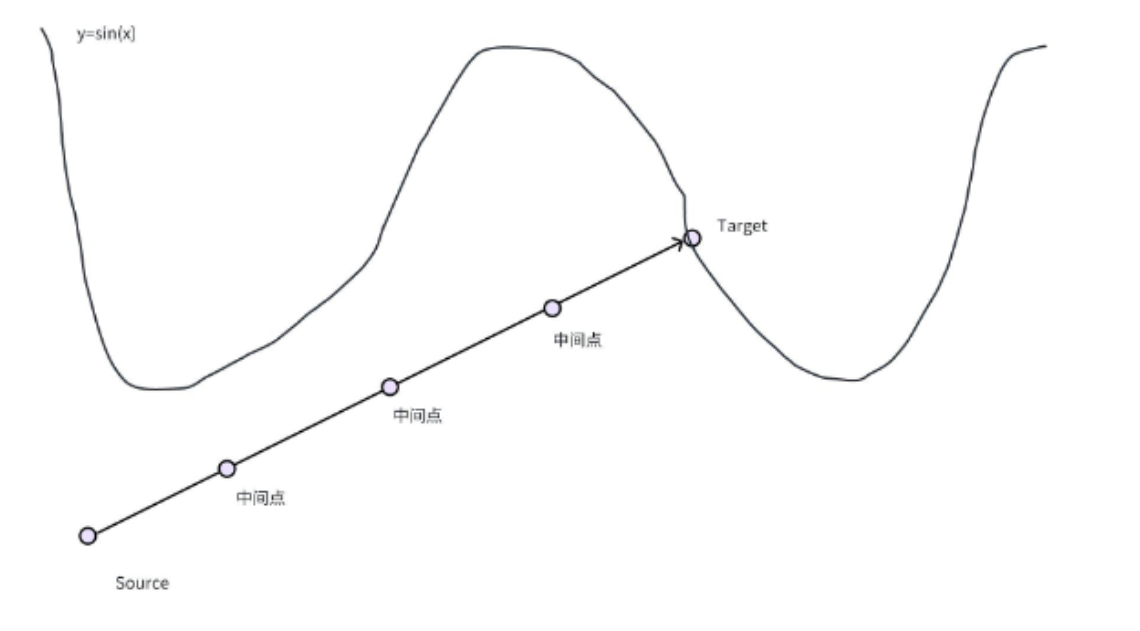
它学习的时候,会在source->target路线上采样出一堆点,然后简单直接的认为source到target这条直线上所有的点,都应该直接朝着target方向走。

ICLR2025: PnP-Flow: Plug-and-Play Image Restoration with Flow Matching
GPT的鼓励:


虽然Flow Matching为分数匹配提供了简单而优雅的替代方案,但仍面临一些重要局限性。
- 采样保证问题。Flow Matching绕过了对数似然计算,而是将模型拟合到速度场。虽然这种方法简化了训练过程,但不再保证生成的样本严格位于目标分布中。这与传统的基于似然的方法形成对比,后者在理论上提供了更强的分布保证。
- 其次是推理时的积分成本。要使用这种方法生成新样本,需要在推理时为每个输入样本求解ODE。与前馈模型或具有较少步骤的扩散采样相比,这在计算上可能是昂贵的,特别是在需要高精度积分的情况下。
- 最后是速度监督的需求。Flow Matching需要访问真实速度信息。虽然这对于简单的合成数据集来说是直接的,但对于现实世界的复杂数据来说,获得准确的速度监督变得极其复杂。
改进方向与扩展
为了解决这些局限性,研究社区已经开发了几种改进方法。
- 带分数模型的Flow Matching方法开始结合两种模型的优势,使用基于分数的目标来训练Flow Matching模型。这种混合方法结合了两个世界的优点,既保持了Flow Matching的简洁性,又获得了分数模型的理论保证。
- 神经ODE求解器的发展为减少推理时间提供了新的可能性。更先进的ODE求解器甚至神经近似器可以通过学习通过流场的高效求解方案来减少推理时间,从而允许在推理时进行更快的采样。

